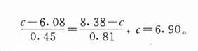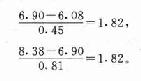流行病学/确定诊断标准
| 流行病学 |
有人对500例健康者和120例肝病病人测定了肝大指数*,数据见附表6-1。二者都接近正态分布,它们的算术平均数和标准差如下:
健康人 χ=6.08,s=0.45;
肝病病人 χ=8.38,s=0.81。
附录6-1 健康人和肝病病人的肝大指数分布
| 肝大指数 | 健康人例数 | 肝病病人例数 | 肝大指数 | 健康人例数 | 肝病病人例数 |
| 4.8- | 3 | 7.8- | 15 | ||
| 5.0- | 12 | 8.0- | 12 | ||
| 5.2- | 24 | 8.2- | 12 | ||
| 5.4- | 43 | 8.4- | 12 | ||
| 5.6- | 51 | 8.6― | 9 | ||
| 5.8- | 62 | 8.8- | 10 | ||
| 6.0- | 96 | 9.0- | 4 | ||
| 6.2- | 91 | 9.2- | 5 | ||
| 6.4- | 63 | 1 | 9.4- | 4 | |
| 6.6- | 31 | - | 9.6- | 2 | |
| 6.8- | 17 | 3 | 9.8- | 1 | |
| 7.0- | 6 | 3 | 10.0- | 6 | |
| 7.2- | 1 | 4 | 12.0- | ||
| 7.4- | 8 | 10.4- | 1 | ||
| 7.6- | 8 | 合计 | 500 | 120 |
由附表6-1可见健康人及肝病病人的肝大指数有部分重叠。不论把诊断标准订在其间何处,都会有漏诊和误诊,或至少会出现其中一种情况。在确定诊断标准时,可按下列要求确定。即用求u值的公式计算。如:
(1)要求缩小漏诊率:即尽量把病人都找出来,然后再进一步确诊。若将漏诊率限定
为1%,可用求u的公式
当漏诊率为1%时,即p/2为0.01时,u=2.326,代入上式
即当肝大指数的诊断标准定为6.50时,漏诊率可以降到1%。但误诊率将升高,结果如下:
漏诊率控制在1%时,可定肝大指数的诊断标准为6.50,但误诊率即升高达17.6%。
(2)要求缩小误诊率:即严格挑选病人。若把误诊率限定为1‰,即P/2为0.001时,u=3.090。
即应把诊断标准定为肝大指数7.47。此时,漏诊率将提高。
![]() ,与此u值相应的P/2=0.132,即漏诊率高达13.2%。
,与此u值相应的P/2=0.132,即漏诊率高达13.2%。
由上可见要求缩小误诊率,漏诊率相应升高。反之也一样。对于筛检来说,漏诊后果严重的病应该用灵敏度较高的方法,而把特异度较高的方法留作临床确诊时用。
(3)要求漏诊率、误诊率都较小:一般把诊断标准定在“漏诊率=误诊率”的位置上。可如下法求此值:
此式即是使c与两个平均值之间的u值相等。
u=1.82时,p/2=0.034,即漏诊率和误诊率都是3.4%。