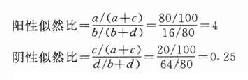流行病学/似然比
| 流行病学 |
某试验阳性的似然比(likelihoodratio,LR)或阳性似然比,如表5-1所示,其计算公式如下。
阳性似然比即正确判断阳性的可能性是错判阳性可能性的倍数。此值愈大,此诊断方法愈好。
阴性似然比即错判断阴性的可能性是正确判断阴性的可能性的倍数。此值愈小,此诊断试验方法愈好。
按180例经手术证实的急性阑尾炎或不是阑尾炎,其右下腹反跳痛的阳性似然比与阴性似然比如下。
表5-6 180例手术证实有、无阑尾炎
| 反跳痛 | 有阑尾炎 | 无阑尾炎 | 合计 |
| 阳 性 | 80 | 16 | 96 |
| 阴 性 | 20 | 64 | 84 |
| 合 计 | 100 | 80 | 180 |
当一名腹痛病人就诊时,如果怀疑该病人患急性阑尾炎的可能性(患病率,验前概率,pretest proba-bility)为50%,则患与不患急性阑尾炎的机遇为1:1(验前概率比,pretestodds)。
验前概率比=验前概率/(1-验前概率)(式5-16)
按此病人应该=0.5/(1-0.5)=1:1
进一步检查有反跳痛,其阳性似然比=4,验后概率比(post-test odds,检查机遇)=验前概率比×阳性似然比(式5-17)=1×4=4。
验后概率(post-testprobability)即该病人患阑尾炎的可能性=验后概率比/(1+验后概率比)=4/(1+4)=80%
结论:病人应该按急性阑尾炎治疗。
如果反跳痛阴性,阴性似然比为0.25。
验后概率比=(1:1)×0.25=0.25:1,该病人患急性阑尾炎的可能性=0.25/(1+0.25)≈0.2=20%。
结论:该病人应当被进一步观察,或做其他检查。
当了解许多症状、体征在某些病的似然比后,可以利用其进行多重试验检验。在进行诊断时,把前一次检验的验后概率作为下一次检验的验前概率,继续运用,直到可下结论为止。举例如下。
一位45岁妇女主诉突发左侧胸痛月余,来门诊就医。该患者是否患冠心病?
查胸痛原因很多,如①肺或胸膜疾患;②上消化道疾病;③冠心病;④情绪影响;⑤其他原因。仅只按其主诉,她患冠心病的可能(验前概率)仅为0.01。
验前概率比=验前概率/(1-验前概率)=0.01/(1-0.01)=0.01。
进一步询问其疼痛特点,有放射至左臂内侧的特点。其阳性似然比为100,此时,其验后概率比=0.01×100=1。
诊断冠心病的概率(验后概率)=验后概率比/(1+验后概率比)=1/(1+1)=0.50=50%。
当再给她做心电图检查,ST段下降2.2mm,其阳性似然比为11,验前概率比=0.5/(1-0.5)=1。验后概率比=1×11=11。验后概率=11/(1+11)=11/12=91.67%。
再进一步检验其血清肌酸磷酸酶(CPK)>80单位,此时阳性似然比为7.75。其验后概率比=[0.9167/(1-0.9167)]×7.75=85.25。验后概率=85.25/(1+85.25)=0.988=98.8%。
经过询问症状,心电图检查及血清CPK检查,该病人患冠心病的可能性为98.8%,因此可以明确诊断该病人患冠心病。